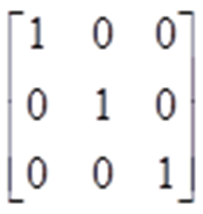Grafika komputer Membuat Perubahan Bentuk Rumah dengan Morphing

Membuat Perubahan Bentuk Rumah dengan Morphing

Oke , pada postingan kali ini aku akan menshare projek morphing yang merupakan implementasi dari materi

Dari listing program diatas saya membuat tiap-tiap objek dari rumah 1 dan rumah 2 dengan mencatat titik-titik dari objek tersebut. Objek dari rumah 1 dan rumah 2 harus lah sama karena agar terlihat seperti adanya perubahan bukan seperti muncul-muncul tiba. Setelah itu baru di proses di bagian fungsi userdraw(). Bagian-bagian dari userdraw mungkin sudah jelas karena telah aku komentar. Semoga bisa menjadi inspirasi ? .

 

Penulis

Ilham Akbar A.H

Read more

Membuat hiasan dengan objek Polar Grafika komputer

Membuat hiasan dengan objek Polar

Kali ini, saya membuat semacam hiasan dengan objek-objek polar. Hampir semua dari objek-objek yang ada pada gambar diatas dibuat dengan objek bulat yang menggunakan rumus-rumus aljabar matematika. Materi untuk membuatan objek-objek diatas dapat kalian lihat apda link berikut http://sayfudinblogz.blogspot.de/2015/06/tutorial-objek-bulat-2d-grafika-komputer.html. Semua objek yang dibuat ada di fungsi userdraw() karena didalam fungsi itu saya hanya memanggil fungsi-fungsi untuk membuat setiap objek .Berikut listing programnya.

Dari listing program diatas terdapat tiga struct yaitu untuk menampung nilai titik atau koordinat dinamai point2D_t, menyimpan warna dinamai color_t, dan menampung vector yang dinamai vector2D_t. Method setColor digunakann untuk menset warna dari suatu objek. Terdapat dua method setColor namun berbeda parameterya, yang satu parameternya float red, float green, dan float blue, sedangkan yang satunya berparameter tipe struct color_t.

Kemudian terdapat berbagai method untuk menggambar objek-objek dari gambar, seperti drawPolyline untuk menggambar garis, drawPolygon untuk menggambar garis juga tapi dengan GL_LINE_LOOP, fillPolygon untuk menggambar objek dengan memberi warna pada dalam objek, gradatePolygon untuk menggambar objek dengan pewarnaan gradasi, centerPolygon untuk menggambar objek dengan pewarnaan terpusat (semua objek pada objek di projek ini menggunakan pewarnaan dengan method ini), drawPolaButterfly untuk menggambar objek dengan bentuk kupu-kupu, drawPola2 untuk memnggambar objek dengan bentuk pola, drawPolaHearth untuk menggambar objek dengan pola hati, drawPolaBunga untuk menggambar objek dengan pola bunga, drawSpiral untuk menggambar objek berbentuk spiral layaknya seperti cangkang keong drawKadiodata untuk menggambar objek dengan bentuk seperti kacang atau kidney, drawCircle untuk menggambar objek dengan pola lingkaran (pada kodingan diatas method ini hanya digunakan untuk mengatur letak dari objek sehingga posisinya dari objek-objeknya melingkar). Semua objek pembentuk objek menggunaka rumusan matematika untuk membentuk objek.

Semua objek yang digambar dipanggil di dalam method userdraw(). Didalam method ini dideklarasi warna dan memanggil method-method yang telah disebutkan diatas.

Penulis Ilham A.H

Read more

Cara membuat Text Dan Font Di OpenGL

 

Di openGL mnyediakan text dan font untuk membuat tulisan jadi kita tidak perlu repot-repot untuk membuat tulisan dari kombinasi garis dan bidang. Jadi begini materinya ,,

A. Karakter Bitmap

OpenGL tidak menyediakan dukungan untuk font dan demikian pula untuk teks. OpenGL menyediakan fungsi untuk bitmap dan fungsi ini dapat dipakai untuk teks. GLUT (dan sistem window yang lain) menyediakan fungsi untuk teks. Fungsi GLUT Bitmap berikut untuk menampilkan teks dengan model *font dan indek karakter ascii (char) :

void glutBitMapCharacter( void *font, int char)

Model font yang dapat dipilih, salah satu dari tabel berikut :

Tabel Konstanta Font Bitmap

No	Konstanta Font Bitmap	Arti	Output
1	GLUT_BITMAP_8_BY_13	Setiap font berukuran 8x13
2	GLUT_BITMAP_9_BY_15	Setiap font berukuran 9x15
3	GLUT_BITMAP_TIMES_ROMAN_10	Setiap font Times Roman, berukuran 10 point
4	GLUT_BITMAP_TIMES_ROMAN_24	Setiap font Times Roman,berukuran 24 point
5	GLUT_BITMAP_HELVETICA_10	Setiap font Helvetica berukuran 10 point
6	GLUT_BITMAP_HELVETICA_12	Setiap font Times Roman, berukuran 12 point
7	GLUT_BITMAP_HELVETICA_18	Setiap font Times Roman, berukuran 18 point

B. Stroke Teks Karakter

Karakter Stoke yang dihasilkan dengan menggunakan primitif OpenGL standar, misalkan garis, poligon, dan kurva. Karakter ini dapat dimodifikasi oleh himpunan transformasi yang dapat diterapkan pada objek geometris. Membuat stroke characters menggunakan fungsi :

void glutStrokeCharacter(void *font, int character);

Parameter font sebagai simbolik karakter menyatakan stroke font yang dipakai (GLUT_STROKE_ROMAN atau GLUT_STROKE_MONO_ROMAN). Sedangkan character adalah karakter yang dibuat.

C. Menempatkan Teks

Untuk menempatkan teks yang telah dibuat dengan glut bitmap atau dengan stroke charakter, digunakan fungsi openGL berikut:

void glRasterPos{234}{sifd}( Type x, Type y, Type z, Type w)

void glRasterPos{234}{sifd}v(TYPE *array)

Penjelasan {234} merujuk pada jumlah parameter fungsi salah satu dari 2,3 atau 4,begitu pula dengan {sifd} berarti tipe parameter single,integer,float,atau double.

Penulis

Ilham A.H

Read more

Grafika Komputer Fungsi Keyboard dan Mouse : Part 3

Fungsi Keyboard dan Mouse : Part 3

Tetap di bidang teknik informatika kususnya di grafika komputer akan melanjutkan tutorial sebagai berikut. Event Handling pada mouse sangat berguna pada semua aplikasi, karena kebanyakan dari interaksi user dengan aplikasi menggunakan mouse seperti mengklik button , atau hover button. Sama halnya dengan openGL penggunaanya juga sama.

OpenGL mempunyai fungsi callback pada saat ada event mouse :

void glutMouseFunc

(void(*func)(int button,int state,int x,int y));

Func adalah sebuah pointer ke fungsi yang membawa 4 parameter integer. Func dipanggil oleh OpenGL ketika mouse ditekan atau dilepas (pressed atau released). Button menyatakan tombol mouse yang ditekan, salah satu dari berikut :

1. GLUT_LEFT_BUTTON

2. GLUT_RIGHT_BUTTON, atau

3. GLUT_MIDDLE_BUTTON

State menyatakan state dari tombol mouse, bernilai salah satunya :

1. GLUT_UP

2. GLUT_DOWN

Sedangkan x dan y menyatakan lokasi (di window : koordinat relatif) dari mouse ketika kejadian.

Fungsi OpenGL untuk event adanya pergerakan pada mouse (mouse motion) adalah:

glutMotionFunc(void(*fuc)(int x,int y));

Func dipanggil oleh OpenGL ketika pointer mouse berpindah di dalam window selama satu atu beberapa button mouse ditekan. Sedangkan x dan y menyatakan lokasi dari mouse ketika kejadian.

Fungsi OpenGL untuk pengecekan tidak adanya event pada mouse (mouse motion) adalah:

glutPassiveMotionFunc(void(*fuc)(int x,int y));

Func dipanggil oleh OpenGL ketika pointer mouse berpindah di dalam window dengan tidak adanya button mouse yang ditekan. Sedangkan x dan y menyatakan lokasi dari mouse ketika kejadian.

Fungsi OpenGL untuk event mouse yang berisi state GLUT_ENTERED atau GLUT_LEFT berdasarkan mouse masuk atau meninggalkan window yaitu:

void glutEntryFunc(void(*func)(int state));

penulis

Ilham A.H

Read more

Grafika Komputer Fungsi Keyboard dan Mouse : Part 2

Fungsi Keyboard dan Mouse : Part 2

Grafika Komputer dalam bidang ilmu teknik Informatika akan membahas kelanjutan dari postingan sebelumnya, kali ini saya akan membahas mengenai even handling yang ada di keyboard. Di event ini banyak digunakan untuk mendesain game , seperti game racing, action, dan genre lainya. Tapi tidak memukinkan untuk digunakna pada keperluan yang lain. Contohnya bisa untuk simulasi. Jadi inilah slah satu kegunaan dari event handling yang ada di keyboard. Jadi , langsung aja ke materi J

OpenGL mempunyai fungsi callback pada saat ada event keyboard :

void glutKeyboardFunc

(void (*func)(unsigned char key, int x, int y));

Func adalah mencatat fungsi yang dipanggil ketika sebuah tombol keyboard di tekan. Parameter key mengembalikan nilai karakter ascii dari tombol keyboard yang ditekan. Koordinat x,y adalah posisi pointer mouse saat keyboard ditekan,yang diukur dari pojok kiri atas window. Sedangkan x dan y menyatakan lokasi (di window : koordinat relatif) dari pointer ketika kejadian key ditekan.

Fungsi OpenGL callback yang lain untuk event adanya keyboard up (pelepasan tombol keyboard) adalah:

void glutKeyboardUpFunc

(void (*func)(unsigned char key, int x, int y));

Func adalah mencatat fungsi yang dipanggil ketika sebuah tombol keyboard selesai ditekan,diangkat. Parameter key mengembalikan nilai karakter ascii dari tombol keyboard yang diangkat. Koordinat x,y adalah posisi pointer mouse saat keyboard ditekan,yang diukur dari pojok kiri atas window. Sedangkan x dan y menyatakan lokasi (di window : koordinat relatif) dari pointer ketika kejadian key ditekan.

Fungsi OpenGL callback yang lain untuk event adanya penekanan pada tombol khusus keyboard adalah:

void glutSpecialFunc

(void (*func)(int key, int x, int y));

Func adalah mencatat fungsi yang dipanggil ketika sebuah tombol keyboard khusus yang ditekan. Parameter key mengembalikan nilai karakter ascii dari tombol keyboard khusus yang ditekan. Koordinat x,y adalah posisi pointer mouse saat keyboard ditekan,yang diukur dari pojok kiri atas window. Sedangkan x dan y menyatakan lokasi (di window : koordinat relatif) dari pointer ketika kejadian key ditekan. Berikut nilai konstanta key dari tombol keyboard khusus yang ditekan dan fungsi tombolnya di keyboard

Tabel Konstanta Key dari Tombol Keyboard Khusus

Konstanta Spesial Key	Fungsi
GLUT_KEY_F1	Key F1
GLUT_KEY_F2	Key F2
GLUT_KEY_F3	Key F3
GLUT_KEY_F4	Key F4
GLUT_KEY_F5	Key F5
GLUT_KEY_F6	Key F6
GLUT_KEY_F7	Key F7
GLUT_KEY_F8	Key F8
GLUT_KEY_F9	Key F9
GLUT_KEY_F10	Key F10
GLUT_KEY_F11	Key F11
GLUT_KEY_F12	Key F12

Tabel Konstanta Key untuk Tombol Keyboard Arah

Konstanta Key Arah	Fungsi
GLUT_KEY_LEFT	Key kiri
GLUT_KEY_UP	Key atas
GLUT_KEY_RIGHT	Key kanan
GLUT_KEY_DOWN	Key bawah
GLUT_KEY_PAGE_UP	Key Page Up
GLUT_KEY_PAGE_DOWN	Key Page Dwon
GLUT_KEY_HOME	Key Home
GLUT_KEY_END	Key End
GLUT_KEY_INSERT	Key Insert

Fungsi OpenGL yang akan mengembalikan salah satu dari nilai konstanta berikut : GLUT_ACTIVE_SHIFT, GLUT_ACTIVE_CTRLatau GLUT_ACTIVE_ALT jika tombol keyboard ini ditekan atau jika ada event mouse yang bekerja.

int glutGetModifiers( )

Selanjutnya akan membahas mengenai even handling yang ada di mouse. So go to this link for the next chapter <kesini >

 

penulis

Ilham A.H

Read more

Grafika komputer Fungsi Keyboard dan Mouse : Part 1

Fungsi Keyboard dan Mouse : Part 1

Grafika komputer didalam bidang teknik informatika Kali ini saya membuat novel serial lagi. Novel ini terdapat 3 bagian. Bagian pertama yang tidak lain melainkan postingan ini berisi event handling yang ada di open gl. Bagian kedua akan membahas mengenai mendefinisikan fungsi keyboard, dan bagian terakhir akan membahas fungsi mouse. So, here I go ,,,

OpenGL menyediakan fungsi yang didefinisikan oleh user dan dipanggil pada saat ada event yang bersesuaian. OpenGL memonitor peralatan input, ketika ada sesuatu yang terjadi,misalkan saat mouse down,key press,dan lain-lain. Pada tabel 4.1 adalah beberapa event yang dicek oleh OpenGL.

Tabel Event di OpenGL

Event	Contoh	Fungsi Callback OpenGL
Keypress	KeyDown KeyUp	glutKeyboardFunc
Mouse	leftButtonDown leftButtonUp	glutMouseFunc
Motion	With mouse press Without	glutMotionFunc glutPassiveMotionFunc
Window	Moving Resizing	glutReshapeFunc
System	Idle Timer	glutIdleFunc glutTimerFunc
Software	What to draw	glutDisplayFunc

Fungsi Callback GLUT adalah fungsi yang berjalan saat ada kejadian (event-driven). Program-program yang menggunakan window untuk input/output,menunggu sampai ada kejadian dan kemudian mengeksekusi beberapa fungsi yang didefinisikan sebelumnya berdasarkan input dari user. Kejadian yang dimaksud : key press,mouse button press dan release,window resize,dan lain-lain. Program OpenGL yang dibuat akan berjalan tak terbatas (infinite loop). Berikut adalah contoh coding program menggunakan input OpenGL. Pembahasan fungsi Callback OpenGL pada praktikum 4 ini akan difokuskan pada pengecekan adanya kejadian mouse motion dan kejadian pada penekanan keyboard. berikut kodenya

int main( intargc, char** argv)

{

glutInit(&argc, argv);

glutInitDisplayMode( GLUT_RGB || GLUT_SINGLE );

glutInitWindowSize( 250, 250 );

glutInitWindowPosition( 100, 100 );

glutCreateWindow(argv[0]);

init ();

glutDisplayFunc( display );

glutReshapeFunc (reshape );

glutMouseFunc( mouse );

glutMotionFunc( motion );

glutKeyboardFunc( keyboard );

glutMainLoop();

return 0;

}

Postingan selanjutnya akan membahas event handling yang ada di keyboard. Langsung aja lanjut ke sini 

Read more

Melakukan Pengesetan Perseptive View dan View Port Fungsi Transformasi : Part 2 Grafika Komputer

Melakukan Pengesetan Perseptive View dan View Port Fungsi Transformasi : Part 2

Teknik informatika memang banyak ilmu yang menarik salah satunya berikut ini. Kelanjutan dari serial sebelumnya , sekuel kali ini , akan membahas bagaimana objek dapat ber-translasi, rotasi, dan scaling. Tentu kalian pernah mendengar istilah ini di saat pelajaran matematika. Yup, benar sekali, semua dari fungsi-fungsi ini mengandung matematika apalagi matriks. Tapi tenang aja, kalian tidak perlu memahami secara betul dari proses matrinya kalau memang bingung , cukup menggunakan fungsi yang tersedia saja. Walau nantinya hanya menggunakan fungsi yang tersedia, tapi kalian perlua tahu gimana dasar dari fungsi itu dibuat. Jadi tunggu apa lagi , here I go ,,,

A. Transformasi di OpenGL

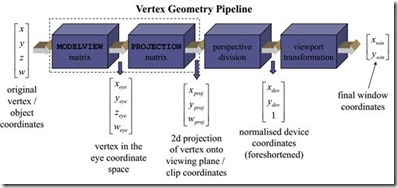
Transformasi vertex di OpenGL sebagai berikut :

Gambar Tahapan Transformasi Vertex di OpenGL

Untuk menggambar sebuah vertex dengan tiga kali transformasi di OpenGL seperti potongan program berikut:

glMatrixMode(GL_MODELVIEW);

glLoadIdentity();// C = I

glMultMatrix(N); // C = N

glMultMatrix(M); // C = NM

glMultMatrix(L); // C = NML

glBegin(GL_POINTS);

glVertex3f(v); // N(M(Lv))

glEnd();

Pernyataan yang ditulis paling akhir akan dioperasikan pertama kali, sedangkan pernyataan yang ditulis di awal dioperasikan terakhir.

Sedangkan matrik transformasi terdiri dari tiga operasi dasar yaitu :

1. Translasi

2. Scaling

3. Rotasi

B. Translasi

Translasi adalah proses perpindahan posisi dari obyek gambar. Formulasi dari proses translasi dapat dijelaskan sebagai berikut:

Gambar 5. 11 Proses translasi

Formulasi translasi adalah:

Bentuk matrik dari proses transformasi di atas dapat dituliskan dengan:

Sehingga matrik transformasi dari proses transalasi adalah:

Untuk membuat fungsi yang menghasilkan matrik translasi ini, terlebih dahulu dibuat fungsi untuk menghasilkan matrik identitas

OpenGL mempunyai fungsi translasi:

void glTranslatef(dx,dy,dz)

Gambar glTranslatef(0.,2.,-2)

C. Scaling

Scaling adalah proses membesarkan/mengecilkan jarak titik sebesar m, yang ditunjukkan oleh gambar 3.12 berikut:

Gambar 5. 13 Proses scaling

Proses scaling dapat dirumuskan dengan:

Secara bentuk matrik formulasi di atas dapat dituliskan dengan:

Dan matrik transformasi dari proses scaling adalah sebagai berikut:

OpenGL mempunyai fungsi scaling:

glScalef(sx,sy,sz)

Gambar 5. 14 glScalef(2.0,-0.5,1.0)

Melakukan skala pada obyek sebesar x,y,z kali sesuai dengan sumbu x,y dan z masing-masing

D. Rotasi

Rotasi adalah proses memutar titik sebesar a^o dengan titik pusat putaran berada pada titik pusat koordinat, yang ditunjukkan oleh gambar 3.13 berikut:

Gambar Proses rotasi

Proses rotasi dapat dirumuskan dengan:

Dan matrik transformasi dari proses rotasi adalah sebagai berikut:

OpenGL mempunyai fungsi rotasi:

void glRotatef*(sudut,x,y,z)

Gambar 5. 16 glRotatef(45.,0.,0.,0.,1.)

Merotasi obyek dengan arah sudut berlawanan arah jarum jam (counterclockwise) dari posisi awal (x,y,z) diputar sebesar sudut.

E. Matrik Identitas

Semua matrik transformasi dibentuk dari matrik indentitas, untuk membuat fungsi yang menghasilkan matrik identitas OpenGL mempunyai fungsi yaitu:

glLoadIdentity()

 

Read more

Melakukan Pengesetan Perseptive View dan View Port Fungsi Transformasi : Part 1 Grafika Komputer

Melakukan Pengesetan Perseptive View dan

View Port Fungsi Transformasi : Part 1

Tetap di Ilmu teknik informatika khususnya grafika komputer. Kali ini aku membuat serial novel lagi. Diserial ini akan membahas ukuran dari hasil projek kita dan koordinat yang diguankan dari projek, tranlasi dan rotas. Namun aku bagi, di part 1 akan membahas mengenai pengesetan perseptive view yang ada di projek. So here I go,,,

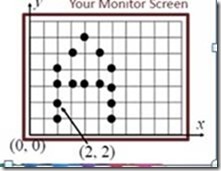
A. Sistem Koordinat Layar

Sistem koordinat layar berbentuk 2D kartesian, dengan pusat (0,0) pada pojok kiri bawah (OpenGL). Piksel didefinisikan pada interseksi kolom dan baris. Didefinisikan relatif pada display layar.

Gambar Sistem Koordinat Layar

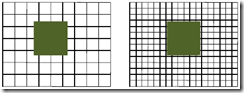
Sistem koordinat layar, pada kenyataannya tidak mudah digunakan karena :

1. Ukuran sistem koordinat layar beraneka ragam

Gambar Contoh representasi 2 sistem koordinat layar yang berbeda

2. Orang lebih suka menggambar berdasarkan ukuran sebenarnya

Gambar Gambar rumah dengan ukuran sebenarnya (feet)

Obyek gambar dalam sistem koordinat riil seharusnya dapat dinyatakan dalam sistem koordinat layar yang terpisah.

B. Menggambar Obyek 2D

Langkah-langkah menggambar obyek 2D sebagai berikut :

1. Obyek gambar dalam sistem koordinat riil

2. Definisikan world window

3. Definisikan screen window

4. Mapping world window ke screen window

Gambar Mapping World Window ke Screen Window

C. Mendefinisikan World Window

World window adalah sebuah daerah kotak di dunia yang ditampilkan ( sistem koordinat world) , perhatikan gambar 3.5.

Gambar 5. 5 World Window

Fungsi OpenGL: 2D Orthogonal Projection,

gluOrtho2D(W_L ,W_R,W_B,W_T)

D. Mendefinisikan Viewport

Viewport window adalah sebuah daerah kotak di layar yang ditampilkan ( sistem koordinat layar) , perhatikan gambar 3.6.

Gambar Mapping World Window ke Viewport

Fungsi OpenGL: 2D Orthogonal Projection,

glViewport(V_L ,V_R,V_B,V_T)

E. Mapping World Window ke Vewport Window

Mapping World Window ke Vewport Window dapat dilakukan hanya dengan pemanggilan dua fungsi OpenGL yaitu:

gluOrtho2D(-1, 1, -1, 1);

glViewport(50, 50, 350, 250);

Perhatikan gambar di bawah ini.

Gambar Mapping World Window ke Vewport Window

F. Rasio Lebar R dan L

Pada Mapping World Window ke Vewport Window rasio lebar R dan L harus sama, sehingga koordinat sx didapatkan dengan formula :

(x-W_L)/(W_R-W_L)=(sx-V_L)/(V_R-V_L)

sx=(x-W_L)(V_R-V_L)/(W_R-W_L)+V_L

Perhatikan gambar dibawah untuk menjaga kesamaan rasio lebar R dan L:

Gambar Kesamaan Rasio Lebar R dan L

G. Rasio Tinggi T dan B

Pada Mapping World Window ke Vewport Window rasio tinggi T dan B harus sama, sehingga koordinat sx didapatkan dengan formula :

(y-W_B)/(W_T-W_B)=(sy-V_B)/(V_T-V_B)

sy=(y-W_B)(V_T-V_B)/(W_R-W_B)+V_B

Perhatikan gambar dibawah untuk menjaga kesamaan rasio tinggi T dan B:

Gambar Kesamaan Rasio Tinggi T dan B

Well , ini sekian dari part 1 ini. Nantikan sekuelnya …

 

penulis

 

Ilham A.H

Read more

Tutorial Objek Bulat 2D grafika komputer

Objek Bulat 2D grafika komputer

Sebelumnya kita telah mempelajari Objek Garis 2D seperti persegi, persgi panjang, segitiga, dll. Nah, pada kali ini tetap di ilmu teknik informatika, saya akan memposting mengenai objek 2D berbentuk bulat seperti linngkaran , elips, dan polar. Perlu diketahui bahwa objek bulat semua menggunakan persamaan matematika. Jadi jika kalian menemukan atau membuat persamaan baru selain yang akan aku post disini akan membentuk bentuk yang baru. So here I go,,,

A. Membuat Lingkaran

Secara definisi, lingkaran adalah segi banyak. Jadi persoalannya disini adalah bagaimana membuat sebuah bangun segi banyak, dimana setiap segi mempunyai sudut yang sama besar. Untuk mempermudah terlebih dahulu diperhatikan sistem koordinat sudut dimana setiap titik dituliskan dengan P(r,a), r adalah jari-jari atau jarak dengan titik pusat dan a adalah sudut.

Gambar 4. 1 Sistem koordinat sudut

Konversi sistem koordinat sudut menjadi sistem koordinat Kartesian adalah sebagai berikut.

Lingkaran adalah suatu bangun yang pada setiap sudutnya, jarak dengan titik pusat selalu sama r.

B. Membuat Ellipse

Ellipse sebenarnya hampir sama dengan lingkaran, hanya saja bedanya adalah pada jari-jari, jika pada lingkaran hanya mengenal satu jari-jari maka ellipse mempunyai dua jari-jari a (arah horisontal) dan b (arah vertikal). Hal inilah yang membuat bentuk ellipse menjadi lonjong.

Gambar 4. 2 Ellips

Persamaan ellips dalam koordinat polar adalah:

C. Membuat Obyek Polar

Obyek polar merupakan obyek benda putar dengan fungsi jari-jari terhadap sudut r=f(q). Perlu proses transformasi dari koordinat polar menjadi koordinat kartesian untuk dapat menggambarkannya pada layar komputer sebagi berikut:

Beberapa bentuk obyek polar,pada tabel berikut :

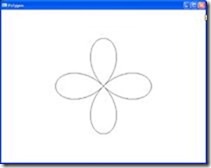
Tabel Fungsi Polar dan Hasil Menggambar Obyek Polar

Fungsi	Hasil
Rose 4 daun:
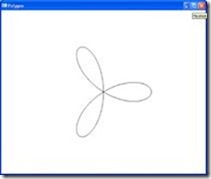
Rose 3 daun:
Kardioda:
Spiral:
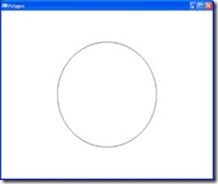
Lingkaran:

Penulis

 

Ilham A.H

Read more